Height and Distance

1. Basic Trigonometric Ratios

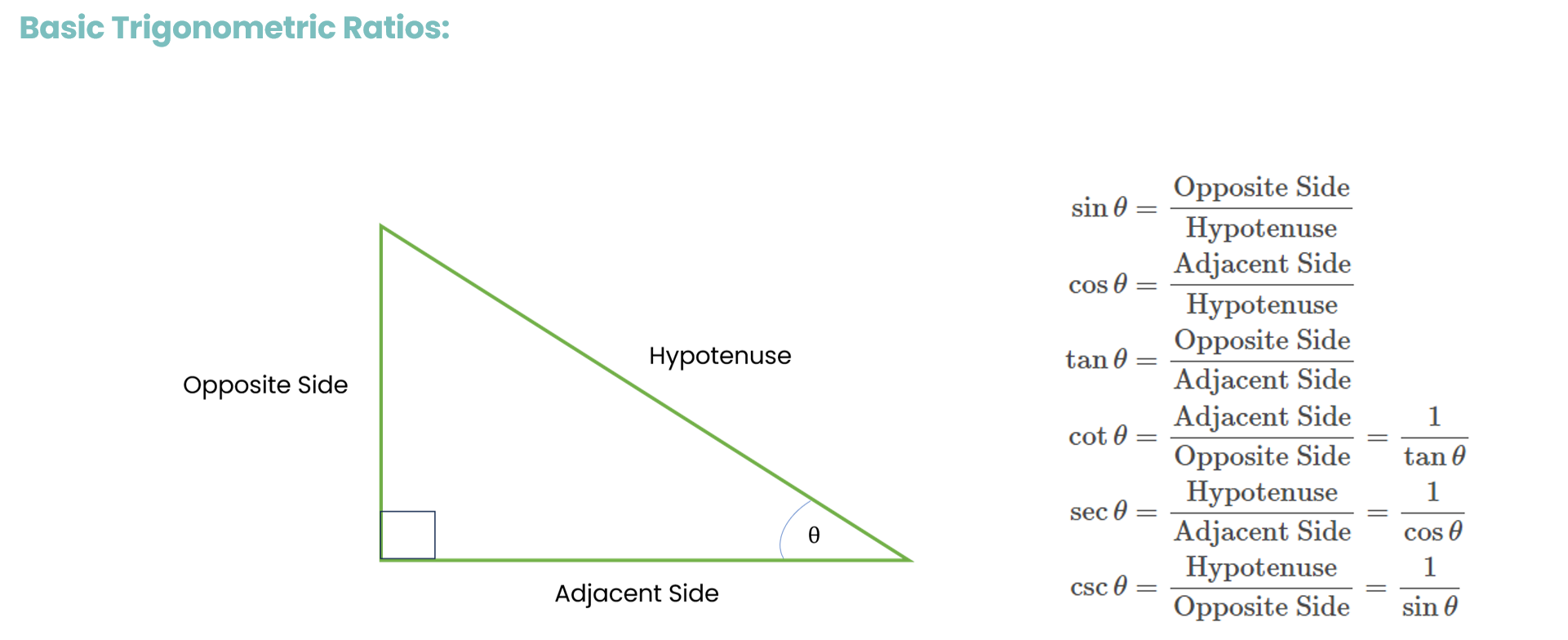
The basic trigonometric ratios are defined as follows:

\[ \begin{align*} \sin \theta &= \frac{\text{Opposite Side}}{\text{Hypotenuse}} \\ \cos \theta &= \frac{\text{Adjacent Side}}{\text{Hypotenuse}} \\ \tan \theta &= \frac{\text{Opposite Side}}{\text{Adjacent Side}} \\ \cot \theta &= \frac{\text{Adjacent Side}}{\text{Opposite Side}} = \frac{1}{\tan \theta} \\ \sec \theta &= \frac{\text{Hypotenuse}}{\text{Adjacent Side}} = \frac{1}{\cos \theta} \\ \csc \theta &= \frac{\text{Hypotenuse}}{\text{Opposite Side}} = \frac{1}{\sin \theta} \end{align*} \]

---

2. Angle of Elevation

The angle of elevation is the angle between the horizontal line and the line of sight looking up to an object.

If a person is looking at the top of a tower from a distance, then:

\[ \tan \theta = \frac{\text{Height of the Object}}{\text{Distance from the Object}} \]

3. Angle of Depression

The angle of depression is the angle between the horizontal line and the line of sight looking down to an object.

If a person is looking at the base of a tower from the top of another tower, then:

\[ \tan \theta = \frac{\text{Height of the Object}}{\text{Distance from the Object}} \]

4. Height of the Object

To find the height of an object when the distance and the angle of elevation are known:

\[ \text{Height} = \text{Distance} \times \tan \theta \]

5. Distance from the Object

To find the distance from the object when the height and the angle of elevation are known:

\[ \text{Distance} = \frac{\text{Height}}{\tan \theta} \]

6. Relationship Between Angles and Sides in a Right-Angled Triangle

For a right-angled triangle with angle \(\theta\), the sides are related by the Pythagorean theorem:

\[ \text{Hypotenuse}^2 = \text{Opposite Side}^2 + \text{Adjacent Side}^2 \]

Additional Formulas for Height and Distance

Finding Height Using Two Angles of Elevation

When the angles of elevation of the top of a tower from two points at a distance \(d\) apart on a horizontal line and in the same vertical plane as the tower are \(\alpha\) and \(\beta\) (\(\alpha > \beta\)), then:

\[ \text{Height of the Tower} = \frac{d \times \tan \alpha \times \tan \beta}{\tan \alpha - \tan \beta} \]

Finding Distance Using Two Angles of Elevation

If the height of a tower is \(h\) and the angles of elevation from two points at a distance \(d\) apart on a horizontal line and in the same vertical plane as the tower are \(\alpha\) and \(\beta\) (\(\alpha > \beta\)), then:

\[ \text{Distance between the two points} = h \left( \frac{1}{\tan \beta} - \frac{1}{\tan \alpha} \right) \]