Non-Deterministic Finite Automata (NFA): An In-Depth Overview

A Non-deterministic Finite Automaton (NFA) is a mathematical model of computation that recognizes a regular language. It is similar to a Deterministic Finite Automaton (DFA) but allows for multiple transitions from a state on the same input symbol, and also allows for ε-transitions, which represent a transition that can be taken without reading any input symbol.

Formally, an NFA is a 5-tuple \((Q, \Sigma, \delta, q_0, F)\), where:

• \(Q\) is a finite set of states.
• \(\Sigma\) is a finite input alphabet.
• \(\delta: Q \times (\Sigma \cup {\epsilon}) \rightarrow 2^Q\) is the transition function that maps a state and an input symbol (or ε) to a set of new states.
• \(q_0 \in Q\) is the initial state.
• \(F \subseteq Q\) is the set of final (or accepting) states.

The transition function \(\delta\) can be extended to a function \( \delta^: Q \times \Sigma^ \rightarrow 2^Q \) that maps a state and a string of input symbols to a set of new states. It is defined recursively as follows:

• \(\delta^*(q, \epsilon) = {q}\) for any state \(q\).
• \( \delta^(q, xa) = \bigcup\limits_{p \in \delta^(q, x)} \delta(p, a) \) for any state \(q\), string \(x \in \Sigma^*\), and symbol \(a \in \Sigma\).

A string \(w \in \Sigma^*\) is accepted by the NFA if there is a sequence of states \(r_0, r_1, \ldots, r_n\) such that:

1. \(r_0 = q_0\)
2. \(r_n \in F\)
3. For each \(i\) between \(0\) and \(n-1\), \(r_{i+1} \in \delta(r_i, a_i)\) for some \(a_i \in \Sigma \cup {\epsilon}\)

The set of strings accepted by an NFA is the set of strings that can be accepted by some sequence of states.

NFAs are useful because they can be smaller than DFAs for some languages, and they can be easier to construct in some cases. However, they are more difficult to simulate than DFAs, and their behavior is less predictable due to the non-deterministic nature of the transitions. Therefore, it is often useful to convert an NFA to an equivalent DFA for practical purposes.

Graphical Representation of an NDFA: (same as DFA)

An NDFA is represented by digraphs called state diagram.

• The vertices represent the states.
• The arcs labeled with an input alphabet show the transitions.
• The initial state is denoted by an empty single incoming arc.
• The final state is indicated by double circles.

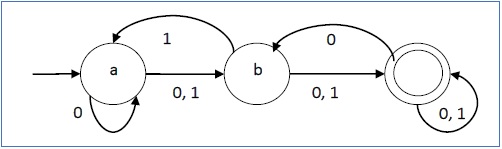
Example

Let a non-deterministic finite automaton be →

• Q = {a, b, c}
• ∑ = {0, 1}
• q₀ = {a}
• F = {c}

The transition function δ as shown below −

Its graphical representation would be as follows −