Deterministic Finite Automata (DFA): Understanding the Basics
Table of Content:
Deterministic finite automata (DFA)
A Deterministic Finite Automaton (DFA) is a mathematical model of computation that recognizes a regular language. It consists of a finite set of states, an input alphabet, a transition function, an initial state, and a set of final (or accepting) states.
At any given time, the DFA is in one of its states. It reads an input symbol from the input alphabet and transitions to a new state based on the current state and the input symbol, according to the transition function. The process repeats until the entire input string is read.
If the final state of the DFA after processing the input string is one of the accepting states, then the input string is accepted by the DFA. Otherwise, the input string is rejected.
DFA has a fixed number of states, which makes it easier to implement and analyze than non-deterministic finite automata (NFA). However, the trade-off is that the number of states required to recognize a language may be exponential in the size of the regular expression describing that language.
DFAs are used in various applications, such as lexical analysis (tokenization) in compilers and regular expression matching in text editors and search engines. They are also useful in studying the properties of regular languages, including closure properties and decision problems.
Formal Definition of DFA
Formally, a Deterministic Finite Automaton (DFA) is a 5-tuple $(Q, \Sigma, \delta, q_0, F)$, where:
- \(Q\) is a finite set of states.
- \(\Sigma\) is a finite input alphabet.
- \(\delta: Q \times \Sigma \rightarrow Q\) is the transition function that maps a state and an input symbol to a new state.
- \(q_0 \in Q\) is the initial state.
- \(F \subseteq Q\) is the set of final (or accepting) states.
The transition function \(\delta\) can be extended to a function \(\delta^: Q \times \Sigma^ \rightarrow Q\) that maps a state and a string of input symbols to a new state. It is defined recursively as follows:
- \(\delta^*(q, \epsilon) = q\) for any state \(q\).
- \(\delta^(q, xa) = \delta(\delta^(q, x), a)\) for any state \(q\), string \(x \in \Sigma^*\), and symbol \(a \in \Sigma\).
The formal definition of a DFA captures the essential properties of the automaton: a set of states, an input alphabet, a transition function, an initial state, and a set of final states. It provides a precise way to describe the behavior of a DFA and allows us to reason about its properties and limitations.
Example
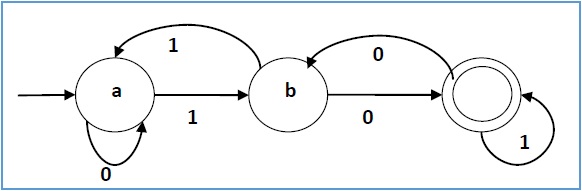
Let a deterministic finite automaton be →
- Q = {a, b, c},
- ∑ = {0, 1},
- q0 = {a},
- F = {c}, and
Transition function δ as shown by the following table −
| Present State | Next State for Input 0 | Next State for Input 1 |
|---|---|---|
| a | a | b |
| b | c | a |
| c | b | c |
Its graphical representation would be as follows −