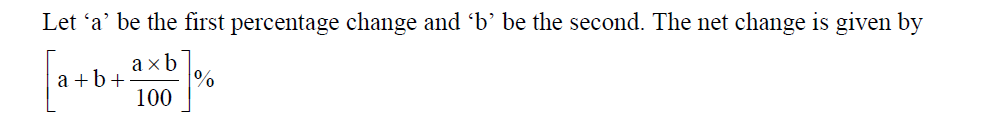- ARs.41
- BRs.42
- CRs.45
- DRs.60
Percentage - Quiz
- A10% profit
- B15% profit
- C10% loss
- D25% loss
- A5% increase
- B15% increase
- C5% decrease
- D15% decrease
Results:
🟢 Correct Answers: 🔴 Wrong Answers:
🟢 Correct Answers: 🔴 Wrong Answers:
Login to save results
Quiz Information
Quiz Information
Quiz Platform FAQ
General Information
- Number of Questions: Each quiz consists of 10 questions.
- Time Limit: You have 30 seconds per question. The total time to complete the quiz is 5 minutes.
- Multiple Attempts: You can take the quiz multiple times to improve your score.
Results and Feedback
- Result Analysis: After completing the quiz, you will see a results page with the following details:
- Correct Option for each question.
- Your Selected Option for each question.
- Explanation for each answer to help you understand why it is correct or incorrect.
- Percentage of Correct Answers to show your overall performance.
- Interactive Features: The platform provides feedback on each attempt to help you learn and improve.
Important Instructions
- Do Not Refresh: Do not refresh the page while taking the quiz. Refreshing the page will end the current quiz and a new quiz will start.
- Saving Your Quiz: To save your quiz progress and questions, log in to your account. Once logged in, you can view saved quizzes in your profile section.
- Mandatory Selection: All questions are mandatory to select. If you do not select all 10 questions, you will not be able to submit the quiz. Once all questions are selected, you will be able to see the Submit button. If you wait until the end of the time, the quiz will be auto-submitted by the system, and you will be able to see your results.
Tips for Taking the Quiz
- Manage Your Time: Keep track of the time for each question to ensure you have enough time to answer all 10 questions.
- Review Explanations: After the quiz, read the explanations provided for each answer to enhance your understanding of the material.
- Retake the Quiz: If desired, take the quiz again to improve your score and reinforce your learning.
- Avoid Refreshing: To prevent losing progress, avoid refreshing the page during the quiz.
- Log In to Save: If you want to save your quiz progress, log in to your account and check your profile section for saved quizzes.
Quiz Analytics
Percentage - Quiz
Guest User Time Taken:
Time Taken: Questions: Answered: Not Answered:
 Correct Answer:
Correct Answer:
 Wrong Answer:
Wrong Answer:
 Percentage: %
Percentage: %
- A. Rs.41
- B. Rs.42
- C. Rs.45
- D. Rs.60
Remarks:
Explanation: Rs.42
Remarks:
Explanation: Useful Formula.
Remarks:
Explanation: Formula for Percentage reduction in consumption
- A. 41%
- B. 42%
- C. 43%
- D. 44%
Remarks:
Explanation: 44%
- A. 2/3
- B. 3/4
- C. 1/2
- D. 5/2
Remarks:
Explanation:
Solve for the original fraction by canceling out the percentage changes. You can start by multiplying both sides of the equation by 92/115 to get (115x/92y) * (92/115) = (15/16) * (92/115) This simplifies to (x/y) = (3/4) So the original fraction is 3/4.
- A. 10000
- B. 15000
- C. 15245
- D. 46888
Remarks:
Explanation:
To find the population size at the beginning of the first year, we can use the formula:
Population at the beginning of the first year = (Total population at the end of the second year) / (1 + (percentage increase)) * (1 - (percentage increase))
Plugging in the values from the given information, we get:
Population at the beginning of the first year = 9975 / (1 + (5/100)) * (1 - (5/100))
Simplifying this expression, we get:
Population at the beginning of the first year = 9975 * (20/21) * (20/19)
Which simplifies to:
Population at the beginning of the first year = 10000
So the population at the beginning of the first year was 10000.
- A. 7%
- B. 11%
- C. 9%
- D. 5%
Remarks:
Explanation:
To solve this problem, you can set up an equation using the given information. Let Z be the percentage of y that is equal to 18% of x. Then: (12/100) * x = (6/100) * y (18/100) * x = (Z/100) * y (9/5) * (6/100) * x = (Z/100) * y Z = (9/5) * 6 Z = 9 Therefore, 9% of y is equal to 18% of x.
- A. 99%
- B. 85%
- C. 88%
- D. 90%
Remarks:
Explanation:
To solve this problem, you can set up an equation using the given information. Let X be the first number, Y be the second number, and Z be the third number. Then: X = (1 - 40/100) * Z Y = (1 - 47/100) * Z (Y/X) = (1 - 47/100) / (1 - 40/100) (Y/X) = (53/100) / (60/100) (Y/X) = (53/60) Y = (53/60) * X Therefore, the second number is approximately 88% of the first number
- A. 10% profit
- B. 15% profit
- C. 10% loss
- D. 25% loss
Remarks:
Explanation:
To write this as an equation, we can define a variable "z" as the net percent change in value. Then we can set up the equation as follows: z = (x + y + xy/100)% = (25 - 12 + (-12 * 25)/100)% = 10% So the equation is: z = 10%
- A. 5% increase
- B. 15% increase
- C. 5% decrease
- D. 15% decrease
Remarks:
Explanation:
we can define a variable "z" as the net percent change in receipts and set up the following equation: z = (x + y + xy/100)% = (-30 + 50 + (-30 * 50)/100)% = 5% This equation shows that the net percent change in receipts is 5%.